Skip to contents

Penalized Precision Matrix Estimation in grasps

Source: vignettes/pen_est.qmd

Preliminary

Consider the following setting:

  • Gaussian graphical model (GGM) assumption:
    The data \(X_{n \times d}\) consists of independent and identically distributed samples \(X_1, \dots, X_n \sim N_d(\mu,\Sigma)\).

  • Disjoint group structure:
    The \(d\) variables can be partitioned into disjoint groups.

  • Goal:
    Estimate the precision matrix \(\Omega = \Sigma^{-1} = (\omega_{ij})_{d \times d}\).

Sparse-Group Estimator

\[\begin{gather} \hat{\Omega}(\lambda,\alpha,\gamma) = {\arg\min}_{\Omega \succ 0} \left\{ -\log\det(\Omega) + \text{tr}(S\Omega) + \lambda P_{\alpha,\gamma}(\Omega) \right\}, \\[10pt] P_{\alpha,\gamma}(\Omega) = \alpha P^\text{idv}_\gamma(\Omega) + (1-\alpha) P^\text{grp}_\gamma(\Omega), \\[10pt] P^\text{idv}_\gamma(\Omega) = \sum_{i,j} p_\gamma(\vert\omega_{ij}\vert), \\[5pt] P^\text{grp}_\gamma(\Omega) = \sum_{g,g^\prime} p_\gamma(\Vert\Omega_{gg^\prime}\Vert_F). \end{gather}\]

where:

  • \(S = n^{-1} \sum_{i=1}^n (X_i-\bar{X})(X_i-\bar{X})^\top\) is the empirical covariance matrix.

  • \(\lambda \geq 0\) is the global regularization parameter controlling overall shrinkage.

  • \(\alpha \in [0,1]\) is the mixing parameter controlling the balance between element-wise and block-wise penalties.

  • \(\gamma\) is the additional parameter controlling the curvature and effective degree of nonconvexity of the penalty.

  • \(P_{\alpha,\gamma}(\Omega)\) is a generic bi-level penalty template that can incorporate convex or non-convex regularizers while preserving the intrinsic group structure among variables.

  • \(P^\text{idv}_\gamma(\Omega)\) is the element-wise individual penalty component.

  • \(P^\text{grp}_\gamma(\Omega)\) is the block-wise group penalty component.

  • \(p_\gamma(\cdot)\) is a penalty kernel parameterized by \(\gamma\).

  • \(\Omega_{gg^\prime}\) is the submatrix of \(\Omega\) with the rows from group \(g\) and columns from group \(g^\prime\).

  • The Frobenius norm \(\Vert\Omega\Vert_F\) is defined as \(\Vert\Omega\Vert_F = (\sum_{i,j} \vert\omega_{ij}\vert^2)^{1/2} = [\text{tr}(\Omega^\top\Omega)]^{1/2}\).

Note:

  • The regularization parameter \(\lambda\) acts as the scale factor for the entire penalty term \(\lambda P_{\alpha,\gamma}(\Omega)\).

  • The penalty kernel \(p_\gamma(\cdot)\) is the shape function that governs the fundamental characteristics of the regularization.

Penalties

  1. Lasso: Least absolute shrinkage and selection operator (Tibshirani 1996; Friedman, Hastie, and Tibshirani 2008)

\[\lambda p(\omega_{ij}) = \lambda\vert\omega_{ij}\vert.\]

  1. Adaptive lasso (Zou 2006; Fan, Feng, and Wu 2009)

\[ \lambda p_\gamma(\omega_{ij}) = \lambda\frac{\vert\omega_{ij}\vert}{v_{ij}}, \] where \(V = (v_{ij})_{d \times d} = (\vert\tilde{\omega}_{ij}\vert^\gamma)_{d \times d}\) is a matrix of adaptive weights, and \(\tilde{\omega}_{ij}\) is the initial estimate obtained using penalty = "lasso".

  1. Atan: Arctangent type penalty (Wang and Zhu 2016)

\[ \lambda p_\gamma(\omega_{ij}) = \lambda(\gamma+\frac{2}{\pi}) \arctan\left(\frac{\vert\omega_{ij}\vert}{\gamma}\right), \quad \gamma > 0. \]

  1. Exp: Exponential type penalty (Wang, Fan, and Zhu 2018)

\[ \lambda p_\gamma(\omega_{ij}) = \lambda\left[1-\exp\left(-\frac{\vert\omega_{ij}\vert}{\gamma}\right)\right], \quad \gamma > 0. \]

  1. Lq (Frank and Friedman 1993; Fu 1998; Fan and Li 2001)

\[ \lambda p_\gamma(\omega_{ij}) = \lambda\vert\omega_{ij}\vert^\gamma, \quad 0 < \gamma < 1. \]

  1. LSP: Log-sum penalty (Candès, Wakin, and Boyd 2008)

\[ \lambda p_\gamma(\omega_{ij}) = \lambda\log\left(1+\frac{\vert\omega_{ij}\vert}{\gamma}\right), \quad \gamma > 0. \]

  1. MCP: Minimax concave penalty (Zhang 2010)

\[ \lambda p_\gamma(\omega_{ij}) = \begin{cases} \lambda\vert\omega_{ij}\vert - \dfrac{\omega_{ij}^2}{2\gamma}, & \text{if } \vert\omega_{ij}\vert \leq \gamma\lambda, \\ \dfrac{1}{2}\gamma\lambda^2, & \text{if } \vert\omega_{ij}\vert > \gamma\lambda. \end{cases} \quad \gamma > 1. \]

  1. SCAD: Smoothly clipped absolute deviation (Fan and Li 2001; Fan, Feng, and Wu 2009)

\[ \lambda p_\gamma(\omega_{ij}) = \begin{cases} \lambda\vert\omega_{ij}\vert & \text{if } \vert\omega_{ij}\vert \leq \lambda, \\ \dfrac{2\gamma\lambda\vert\omega_{ij}\vert-\omega_{ij}^2-\lambda^2}{2(\gamma-1)} & \text{if } \lambda < \vert\omega_{ij}\vert < \gamma\lambda, \\ \dfrac{\lambda^2(\gamma+1)}{2} & \text{if } \vert\omega_{ij}\vert \geq \gamma\lambda. \end{cases} \quad \gamma > 2. \]

Note:

  • For Lasso, which is convex, the additional parameter \(\gamma\) is not required, and the penalty kernel \(p_\gamma(\cdot)\) simplifies to \(p(\cdot)\).

  • For MCP and SCAD, \(\lambda\) plays a dual role: it is the global regularization parameter, but it is also implicitly contained within the kernel \(p_\gamma(\cdot)\).

Illustrative Visualization

Figure 1 illustrates a comparison of various penalty functions \(\lambda p(\omega)\) evaluated over a range of \(\omega\) values. The main panel (right) provides a wider view of the penalty functions’ behavior for larger \(\vert\omega\vert\), while the inset panel (left) magnifies the region near zero \([-1, 1]\).

library(grasps) ## for penalty computation
library(ggplot2) ## for visualization

penalties <- c("atan", "exp", "lasso", "lq", "lsp", "mcp", "scad")

pen_df <- compute_penalty(seq(-4, 4, by = 0.01), penalties, lambda = 1)
plot(pen_df, xlim = c(-1, 1), ylim = c(0, 1), zoom.size = 1) +
  guides(color = guide_legend(nrow = 2, byrow = TRUE))

Figure 1: Illustrative penalty functions.

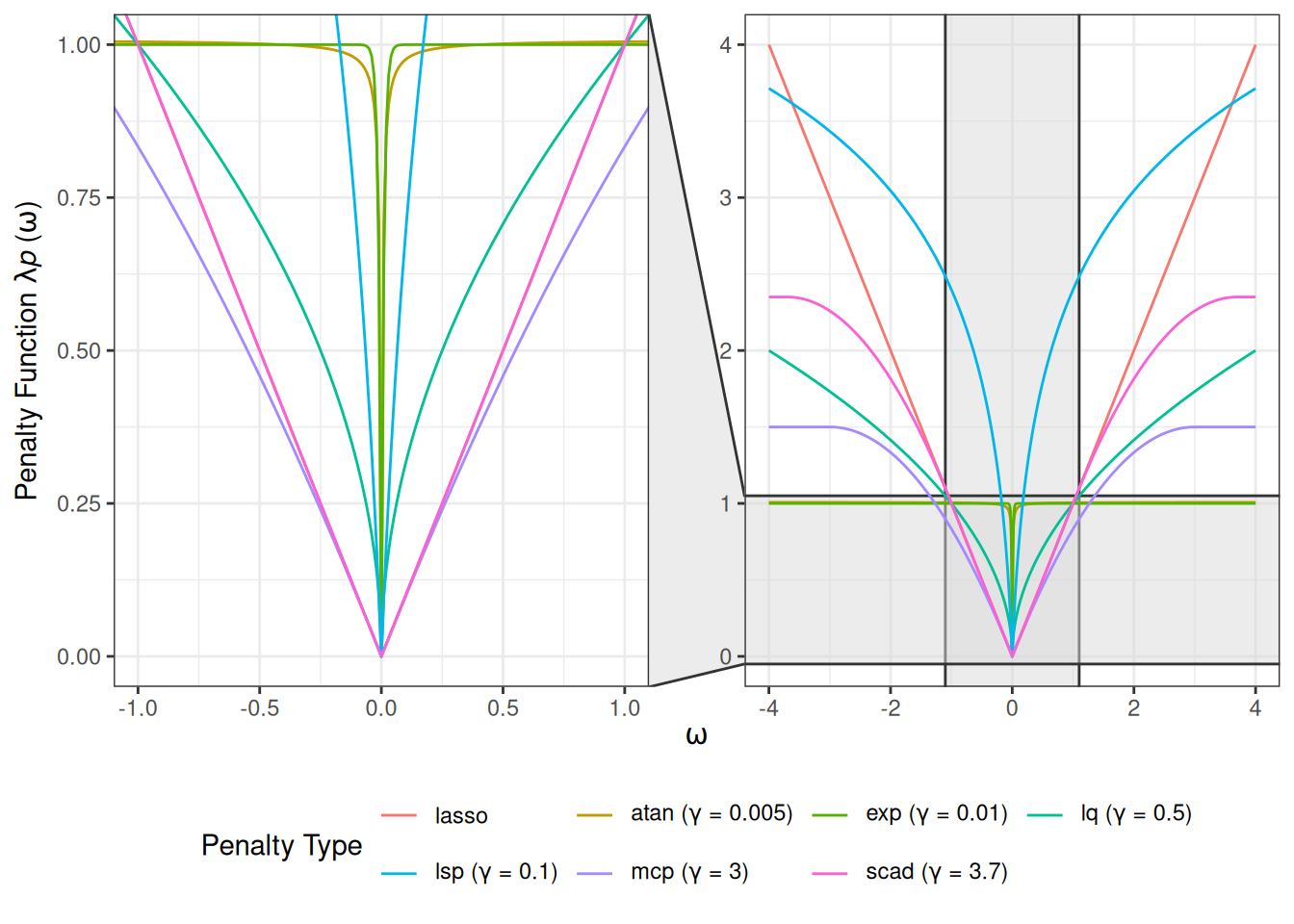
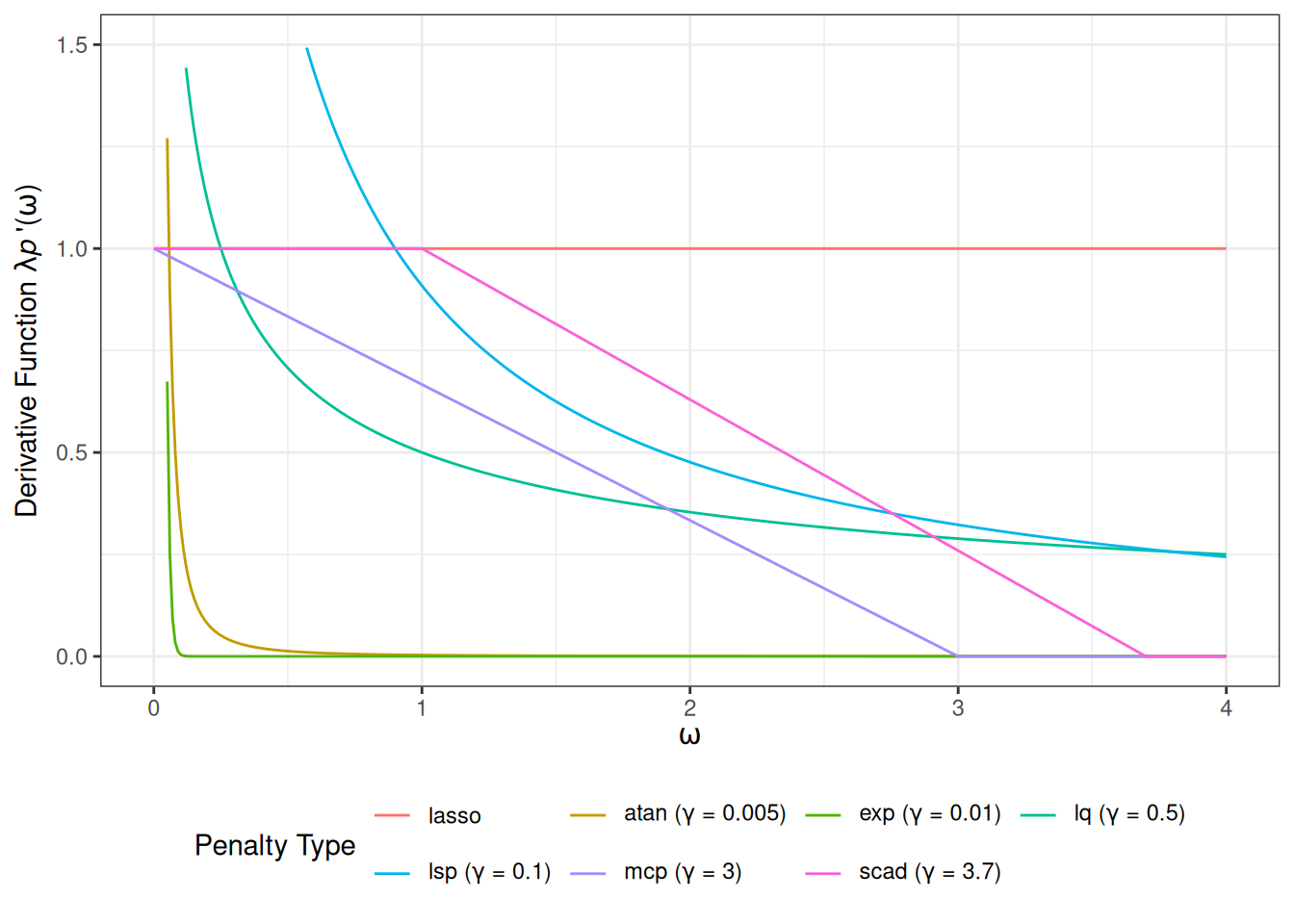
Figure 2 displays the derivative function \(p^\prime(\omega)\) associated with a range of penalty types. The Lasso exhibits a constant derivative, corresponding to uniform shrinkage. For MCP and SCAD, the derivatives are piecewise: initially equal to the Lasso derivative, then decreasing over an intermediate region, and eventually dropping to zero, indicating that large \(\vert\omega\vert\) receive no shrinkage. Other non-convex penalties show smoothly diminishing derivatives as \(\vert\omega\vert\) increases, reflecting their tendency to shrink small \(\vert\omega\vert\) strongly while exerting little to no shrinkage on large ones.

deriv_df <- compute_derivative(seq(0, 4, by = 0.01), penalties, lambda = 1)
plot(deriv_df) +
  scale_y_continuous(limits = c(0, 1.5)) +
  guides(color = guide_legend(nrow = 2, byrow = TRUE))

Figure 2: Illustrative penalty derivatives.

Reference

Candès, Emmanuel J., Michael B. Wakin, and Stephen P. Boyd. 2008. “Enhancing Sparsity by Reweighted \(\ell_1\) Minimization.” Journal of Fourier Analysis and Applications 14 (5): 877–905. https://doi.org/10.1007/s00041-008-9045-x.
Fan, Jianqing, Yang Feng, and Yichao Wu. 2009. “Network Exploration via the Adaptive LASSO and SCAD Penalties.” The Annals of Applied Statistics 3 (2): 521–41. https://doi.org/10.1214/08-aoas215.
Fan, Jianqing, and Runze Li. 2001. “Variable Selection via Nonconcave Penalized Likelihood and Its Oracle Properties.” Journal of the American Statistical Association 96 (456): 1348–60. https://doi.org/10.1198/016214501753382273.
Frank, Lldiko E., and Jerome H. Friedman. 1993. “A Statistical View of Some Chemometrics Regression Tools.” Technometrics 35 (2): 109–35. https://doi.org/10.1080/00401706.1993.10485033.
Friedman, Jerome, Trevor Hastie, and Robert Tibshirani. 2008. “Sparse Inverse Covariance Estimation with the Graphical Lasso.” Biostatistics 9 (3): 432–41. https://doi.org/10.1093/biostatistics/kxm045.
Fu, Wenjiang J. 1998. “Penalized Regressions: The Bridge Versus the Lasso.” Journal of Computational and Graphical Statistics 7 (3): 397–416. https://doi.org/10.1080/10618600.1998.10474784.
Tibshirani, Robert. 1996. “Regression Shrinkage and Selection via the Lasso.” Journal of the Royal Statistical Society: Series B (Methodological) 58 (1): 267–88. https://doi.org/10.1111/j.2517-6161.1996.tb02080.x.
Wang, Yanxin, Qibin Fan, and Li Zhu. 2018. “Variable Selection and Estimation Using a Continuous Approximation to the \(L_0\) Penalty.” Annals of the Institute of Statistical Mathematics 70 (1): 191–214. https://doi.org/10.1007/s10463-016-0588-3.
Wang, Yanxin, and Li Zhu. 2016. “Variable Selection and Parameter Estimation with the Atan Regularization Method.” Journal of Probability and Statistics 2016: 6495417. https://doi.org/10.1155/2016/6495417.
Zhang, Cun-Hui. 2010. “Nearly Unbiased Variable Selection Under Minimax Concave Penalty.” The Annals of Statistics 38 (2): 894–942. https://doi.org/10.1214/09-AOS729.
Zou, Hui. 2006. “The Adaptive Lasso and Its Oracle Properties.” Journal of the American Statistical Association 101 (476): 1418–29. https://doi.org/10.1198/016214506000000735.