Skip to contents

Penalty Derivative Computation

Source: R/compute_derivative.R
compute_derivative.Rd

Compute one or more derivative values for a given omega, allowing vectorized specifications of penalty, lambda, and gamma.

Usage

compute_derivative(omega, penalty, lambda, gamma = NA)

Arguments

omega

A numeric value or vector at which the penalty is evaluated.

penalty

A character string or vector specifying one or more penalty types. Available options include:

  1. "lasso": Least absolute shrinkage and selection operator (Tibshirani 1996; Friedman et al. 2008) .

  2. "atan": Arctangent type penalty (Wang and Zhu 2016) .

  3. "exp": Exponential type penalty (Wang et al. 2018) .

  4. "lq": Lq penalty (Frank and Friedman 1993; Fu 1998; Fan and Li 2001) .

  5. "lsp": Log-sum penalty (Candès et al. 2008) .

  6. "mcp": Minimax concave penalty (Zhang 2010) .

  7. "scad": Smoothly clipped absolute deviation (Fan and Li 2001; Fan et al. 2009) .

If penalty has length 1, it is recycled to the common length determined by penalty, lambda, and gamma.

lambda

A non-negative numeric value or vector specifying the regularization parameter. If lambda has length 1, it is recycled to the common length determined by penalty, lambda, and gamma.

gamma

A numeric value or vector specifying the additional parameter for the penalty function. If lambda has length 1, it is recycled to the common length determined by penalty, lambda, and gamma. The penalty-specific defaults are:

  1. "atan": 0.005

  2. "exp": 0.01

  3. "lq": 0.5

  4. "lsp": 0.1

  5. "mcp": 3

  6. "scad": 3.7

For "lasso", gamma is ignored.

Value

A data frame with S3 class "derivative" containing:

omega

The input omega values.

penalty

The penalty type for each row.

lambda

The regularization parameter used.

gamma

The additional penalty parameter used.

value

The computed derivative value.

The number of rows equals max(length(penalty), length(lambda), length(gamma)). Any of penalty, lambda, or gamma with length 1 is recycled to this common length.

References

Candès EJ, Wakin MB, Boyd SP (2008). “Enhancing Sparsity by Reweighted \(\ell_1\) Minimization.” Journal of Fourier Analysis and Applications, 14(5), 877–905. doi:10.1007/s00041-008-9045-x .

Fan J, Feng Y, Wu Y (2009). “Network Exploration via the Adaptive LASSO and SCAD Penalties.” The Annals of Applied Statistics, 3(2), 521–541. doi:10.1214/08-aoas215 .

Fan J, Li R (2001). “Variable Selection via Nonconcave Penalized Likelihood and its Oracle Properties.” Journal of the American Statistical Association, 96(456), 1348–1360. doi:10.1198/016214501753382273 .

Frank LE, Friedman JH (1993). “A Statistical View of Some Chemometrics Regression Tools.” Technometrics, 35(2), 109–135. doi:10.1080/00401706.1993.10485033 .

Friedman J, Hastie T, Tibshirani R (2008). “Sparse Inverse Covariance Estimation with the Graphical Lasso.” Biostatistics, 9(3), 432–441. doi:10.1093/biostatistics/kxm045 .

Fu WJ (1998). “Penalized Regressions: The Bridge versus the Lasso.” Journal of Computational and Graphical Statistics, 7(3), 397–416. doi:10.1080/10618600.1998.10474784 .

Tibshirani R (1996). “Regression Shrinkage and Selection via the Lasso.” Journal of the Royal Statistical Society: Series B (Methodological), 58(1), 267–288. doi:10.1111/j.2517-6161.1996.tb02080.x .

Wang Y, Fan Q, Zhu L (2018). “Variable Selection and Estimation using a Continuous Approximation to the \(L_0\) Penalty.” Annals of the Institute of Statistical Mathematics, 70(1), 191–214. doi:10.1007/s10463-016-0588-3 .

Wang Y, Zhu L (2016). “Variable Selection and Parameter Estimation with the Atan Regularization Method.” Journal of Probability and Statistics, 2016, 6495417. doi:10.1155/2016/6495417 .

Zhang C (2010). “Nearly Unbiased Variable Selection under Minimax Concave Penalty.” The Annals of Statistics, 38(2), 894–942. doi:10.1214/09-AOS729 .

Examples

library(grasps)
library(ggplot2)

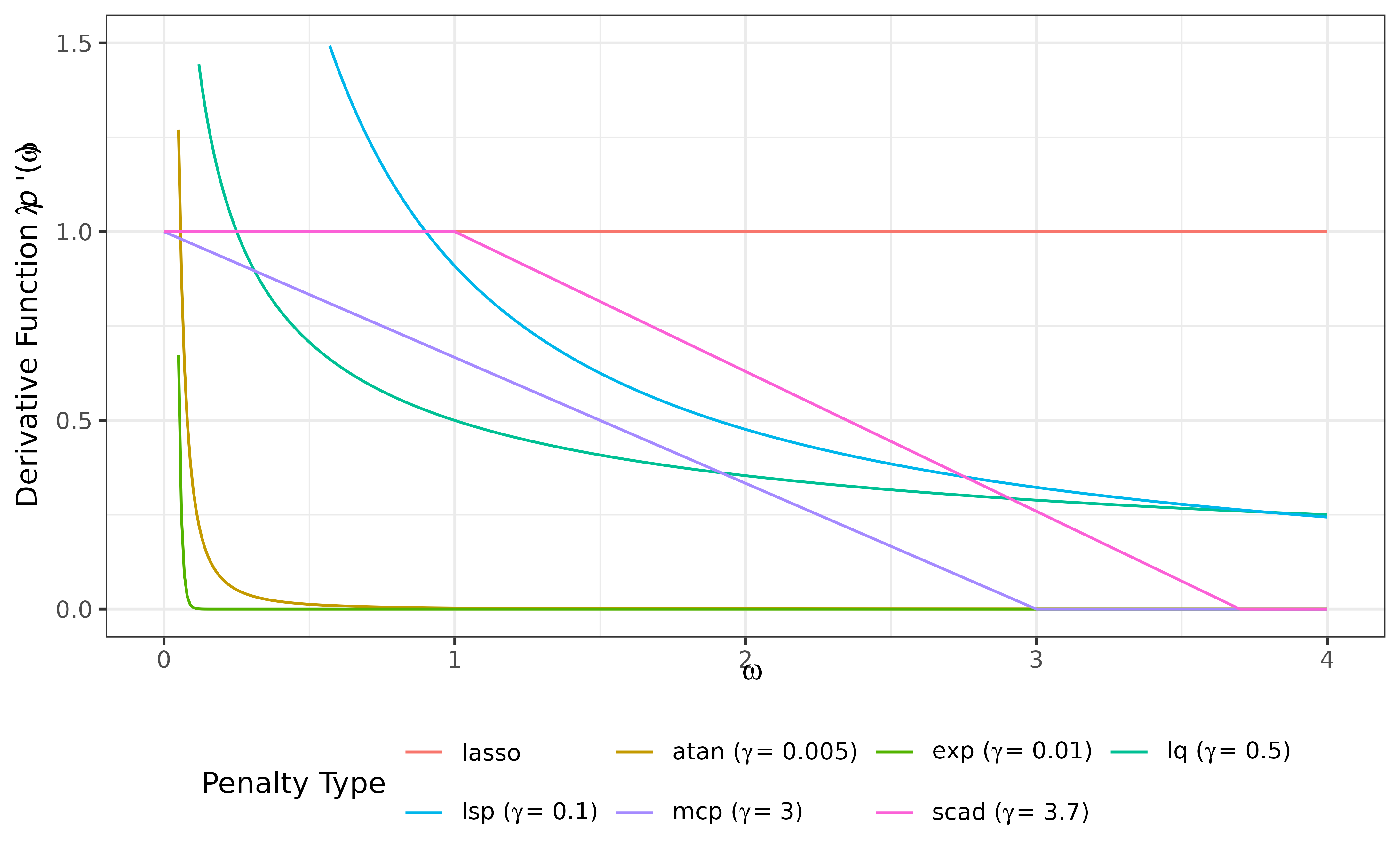
deriv_df <- compute_derivative(
  omega = seq(0, 4, by = 0.01),
  penalty = c("atan", "exp", "lasso", "lq", "lsp", "mcp", "scad"),
  lambda = 1)

plot(deriv_df) +
  scale_y_continuous(limits = c(0, 1.5)) +
  guides(color = guide_legend(nrow = 2, byrow = TRUE))
#> Warning: Removed 79 rows containing missing values or values outside the scale range
#> (`geom_line()`).