Groupwise Regularized Adaptive Sparse Precision Solution

Provide a collection of statistical methods that incorporate both element-wise and group-wise penalties to estimate a precision matrix.

Usage

grasps(
  X,
  n = nrow(X),
  membership,
  penalty,
  diag.ind = TRUE,
  diag.grp = TRUE,
  diag.include = FALSE,
  lambda = NULL,
  alpha = NULL,
  gamma = NULL,
  nlambda = 10,
  lambda.min.ratio = 0.01,
  growiter.lambda = 30,
  tol.lambda = 0.001,
  maxiter.lambda = 50,
  rho = 2,
  tau.incr = 2,
  tau.decr = 2,
  nu = 10,
  tol.abs = 1e-04,
  tol.rel = 1e-04,
  maxiter = 10000,
  crit = "BIC",
  kfold = 5,
  ebic.tuning = 0.5
)

Arguments

X

An \(n \times d\) data matrix with sample size \(n\) and dimension \(d\).
A \(d \times d\) sample covariance matrix with dimension \(d\).

n

An integer (default = nrow(X)) specifying the sample size. This is only required when the input matrix X is a \(d \times d\) sample covariance matrix with dimension \(d\).

membership

An integer vector specifying the group membership. The length of membership must be consistent with the dimension \(d\).

penalty

A character string specifying the penalty for estimating precision matrix. Available options include:

"lasso": Least absolute shrinkage and selection operator (Tibshirani 1996; Friedman et al. 2008) .
"adapt": Adaptive lasso (Zou 2006; Fan et al. 2009) .
"atan": Arctangent type penalty (Wang and Zhu 2016) .
"exp": Exponential type penalty (Wang et al. 2018) .
"lq": Lq penalty (Frank and Friedman 1993; Fu 1998; Fan and Li 2001) .
"lsp": Log-sum penalty (Candès et al. 2008) .
"mcp": Minimax concave penalty (Zhang 2010) .
"scad": Smoothly clipped absolute deviation (Fan and Li 2001; Fan et al. 2009) .

diag.ind

A logical value (default = TRUE) specifying whether to penalize the diagonal elements.

diag.grp

A logical value (default = TRUE) specifying whether to penalize the within-group blocks.

diag.include

A logical value (default = FALSE) specifying whether to include the diagonal entries in the penalty for within-group blocks when diag.grp = TRUE.

lambda

A non-negative numeric vector specifying the grid for the regularization parameter. The default is NULL, which generates its own lambda sequence based on nlambda and lambda.min.ratio.

alpha

A numeric vector in [0, 1] specifying the grid for the mixing parameter balancing the element-wise individual L1 penalty and the block-wise group L2 penalty. An alpha of 1 corresponds to the individual penalty only; an alpha of 0 corresponds to the group penalty only. The default value is a sequence from 0.1 to 0.9 with increments of 0.1.

gamma

A numeric value specifying the additional parameter fo the chosen penalty. The default value depends on the penalty:

"adapt": 0.5
"atan": 0.005
"exp": 0.01
"lq": 0.5
"lsp": 0.1
"mcp": 3
"scad": 3.7

nlambda

An integer (default = 10) specifying the number of lambda values to generate when lambda = NULL.

lambda.min.ratio

A numeric value > 0 (default = 0.01) specifying the fraction of the maximum lambda value \(\lambda_{max}\) to generate the minimum lambda \(\lambda_{min}\). If lambda = NULL, a lambda grid of length nlambda is automatically generated on a log scale, ranging from \(\lambda_{max}\) down to \(\lambda_{min}\).

growiter.lambda

An integer (default = 30) specifying the maximum number of exponential growth steps during the initial search for an admissible upper bound \(\lambda_{\max}\).

tol.lambda

A numeric value > 0 (default = 1e-03) specifying the relative tolerance for the bisection stopping rule on the interval width.

maxiter.lambda

An integer (default = 50) specifying the maximum number of bisection iterations in the line search for \(\lambda_{\max}\).

rho

A numeric value > 0 (default = 2) specifying the ADMM augmented-Lagrangian penalty parameter (often called the ADMM step size). Larger values typically put more weight on enforcing the consensus constraints at each iteration; smaller values yield more conservative updates.

tau.incr

A numeric value > 1 (default = 2) specifying the multiplicative factor used to increase rho when the primal residual dominates the dual residual in ADMM.

tau.decr

A numeric value > 1 (default = 2) specifying the multiplicative factor used to decrease rho when the dual residual dominates the primal residual in ADMM.

nu

A numeric value > 1 (default = 10) controlling how aggressively rho is rescaled in the adaptive-rho scheme (residual balancing).

tol.abs

A numeric value > 0 (default = 1e-04) specifying the absolute tolerance for ADMM stopping (applied to primal/dual residual norms).

tol.rel

A numeric value > 0 (default = 1e-04) specifying the relative tolerance for ADMM stopping (applied to primal/dual residual norms).

maxiter

An integer (default = 1e+04) specifying the maximum number of ADMM iterations.

crit

A character string (default = "BIC") specifying the parameter selection criterion to use. Available options include:

"AIC": Akaike information criterion (Akaike 1973) .
"BIC": Bayesian information criterion (Schwarz 1978) .
"EBIC": extended Bayesian information criterion (Chen and Chen 2008; Foygel and Drton 2010) .
"HBIC": high dimensional Bayesian information criterion (Wang et al. 2013; Fan et al. 2017) .
"CV": k-fold cross validation with negative log-likelihood loss.

kfold

An integer (default = 5) specifying the number of folds used for crit = "CV".

ebic.tuning

A numeric value in [0, 1] (default = 0.5) specifying the tuning parameter to calculate for crit = "EBIC".

Value

An object with S3 class "grasps" containing the following components:

hatOmega: The estimated precision matrix.
lambda: The optimal regularization parameter.
alpha: The optimal mixing parameter.
initial: The initial estimate of hatOmega when a non-convex penalty is chosen via penalty.
gamma: The optimal addtional parameter when a non-convex penalty is chosen via penalty.
iterations: The number of ADMM iterations.
lambda.grid: The actual lambda grid used in the program.
alpha.grid: The actual alpha grid used in the program.
lambda.safe: The bisection-refined upper bound \(\lambda_{\max}\), corresponding to alpha.grid, when lambda = NULL.
loss: The optimal k-fold loss when crit = "CV".
CV.loss: Matrix of CV losses, with rows for parameter combinations and columns for CV folds, when crit = "CV".
score: The optimal information criterion score when crit is set to "AIC", "BIC", "EBIC", or "HBIC".
IC.score: The information criterion score for each parameter combination when crit is set to "AIC", "BIC", "EBIC", or "HBIC".
membership: The group membership.

References

Akaike H (1973). “Information Theory and an Extension of the Maximum Likelihood Principle.” In Petrov BN, Csáki F (eds.), Second International Symposium on Information Theory, 267–281. Akad\'emiai Kiad\'o, Budapest, Hungary.

Candès EJ, Wakin MB, Boyd SP (2008). “Enhancing Sparsity by Reweighted \(\ell_1\) Minimization.” Journal of Fourier Analysis and Applications, 14(5), 877–905. doi:10.1007/s00041-008-9045-x .

Chen J, Chen Z (2008). “Extended Bayesian Information Criteria for Model Selection with Large Model Spaces.” Biometrika, 95(3), 759–771. doi:10.1093/biomet/asn034 .

Fan J, Feng Y, Wu Y (2009). “Network Exploration via the Adaptive LASSO and SCAD Penalties.” The Annals of Applied Statistics, 3(2), 521–541. doi:10.1214/08-aoas215 .

Fan J, Li R (2001). “Variable Selection via Nonconcave Penalized Likelihood and its Oracle Properties.” Journal of the American Statistical Association, 96(456), 1348–1360. doi:10.1198/016214501753382273 .

Fan J, Liu H, Ning Y, Zou H (2017). “High Dimensional Semiparametric Latent Graphical Model for Mixed Data.” Journal of the Royal Statistical Society Series B: Statistical Methodology, 79(2), 405–421. doi:10.1111/rssb.12168 .

Foygel R, Drton M (2010). “Extended Bayesian Information Criteria for Gaussian Graphical Models.” In Lafferty J, Williams C, Shawe-Taylor J, Zemel R, Culotta A (eds.), Advances in Neural Information Processing Systems 23 (NIPS 2010), 604–612. https://dl.acm.org/doi/10.5555/2997189.2997257.

Frank LE, Friedman JH (1993). “A Statistical View of Some Chemometrics Regression Tools.” Technometrics, 35(2), 109–135. doi:10.1080/00401706.1993.10485033 .

Friedman J, Hastie T, Tibshirani R (2008). “Sparse Inverse Covariance Estimation with the Graphical Lasso.” Biostatistics, 9(3), 432–441. doi:10.1093/biostatistics/kxm045 .

Fu WJ (1998). “Penalized Regressions: The Bridge versus the Lasso.” Journal of Computational and Graphical Statistics, 7(3), 397–416. doi:10.1080/10618600.1998.10474784 .

Schwarz G (1978). “Estimating the Dimension of a Model.” The Annals of Statistics, 6(2), 461–464. doi:10.1214/aos/1176344136 .

Tibshirani R (1996). “Regression Shrinkage and Selection via the Lasso.” Journal of the Royal Statistical Society: Series B (Methodological), 58(1), 267–288. doi:10.1111/j.2517-6161.1996.tb02080.x .

Wang L, Kim Y, Li R (2013). “Calibrating Nonconvex Penalized Regression in Ultra-High Dimension.” The Annals of Statistics, 41(5), 2505–2536. doi:10.1214/13-AOS1159 .

Wang Y, Fan Q, Zhu L (2018). “Variable Selection and Estimation using a Continuous Approximation to the \(L_0\) Penalty.” Annals of the Institute of Statistical Mathematics, 70(1), 191–214. doi:10.1007/s10463-016-0588-3 .

Wang Y, Zhu L (2016). “Variable Selection and Parameter Estimation with the Atan Regularization Method.” Journal of Probability and Statistics, 2016, 6495417. doi:10.1155/2016/6495417 .

Zhang C (2010). “Nearly Unbiased Variable Selection under Minimax Concave Penalty.” The Annals of Statistics, 38(2), 894–942. doi:10.1214/09-AOS729 .

Zou H (2006). “The Adaptive Lasso and Its Oracle Properties.” Journal of the American Statistical Association, 101(476), 1418–1429. doi:10.1198/016214506000000735 .

Examples

library(grasps)

## reproducibility for everything
set.seed(1234)

## block-structured precision matrix based on SBM
sim <- gen_prec_sbm(d = 30, K = 3,
                    within.prob = 0.25, between.prob = 0.05,
                    weight.dists = list("gamma", "unif"),
                    weight.paras = list(c(shape = 20, rate = 10),
                                        c(min = 0, max = 5)),
                    cond.target = 100)
## visualization
plot(sim)


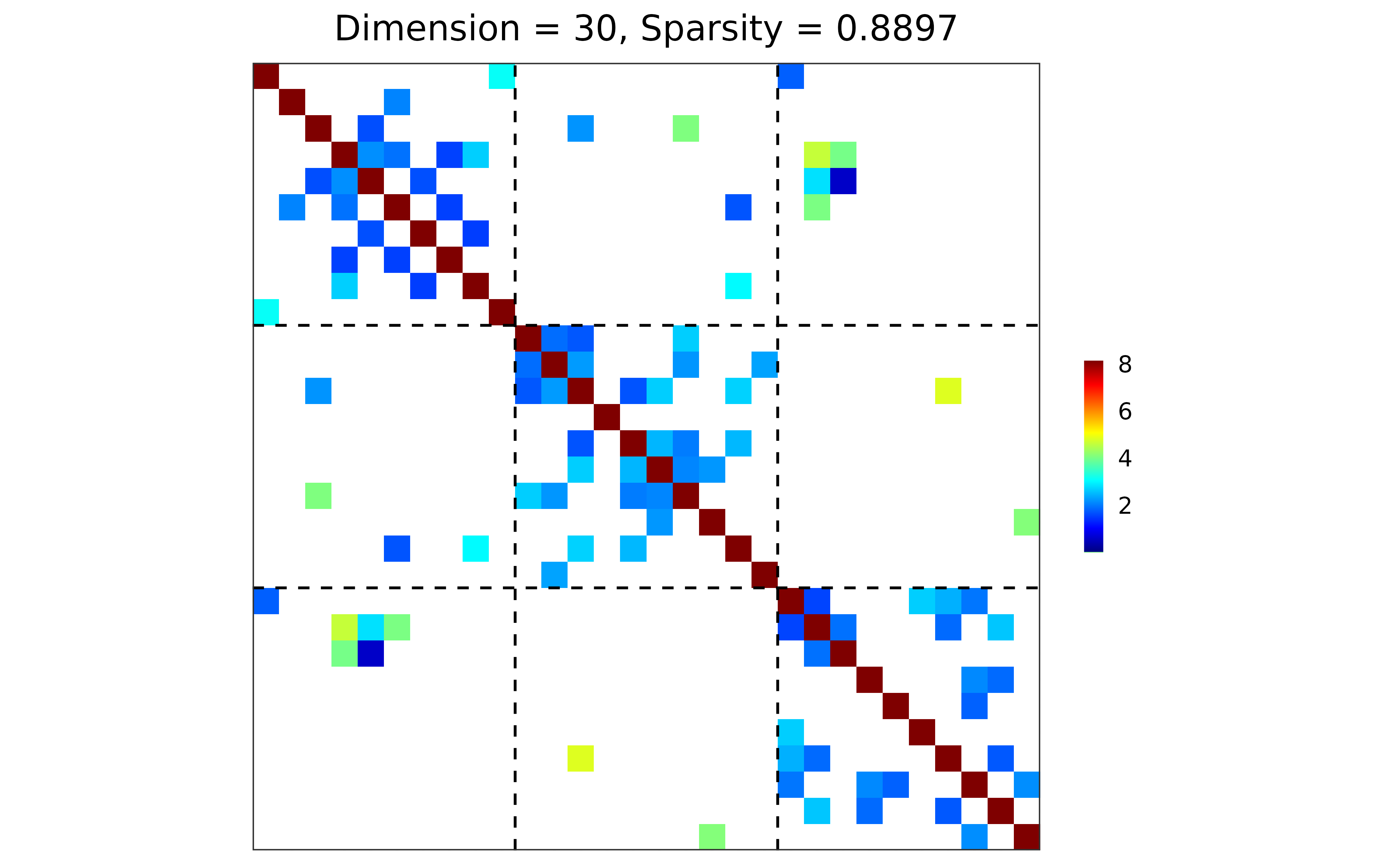## n-by-d data matrix
library(MASS)
X <- mvrnorm(n = 20, mu = rep(0, 30), Sigma = sim$Sigma)

## adapt, HBIC
res <- grasps(X = X, membership = sim$membership, penalty = "adapt", crit = "HBIC")

## visualization
plot(res)


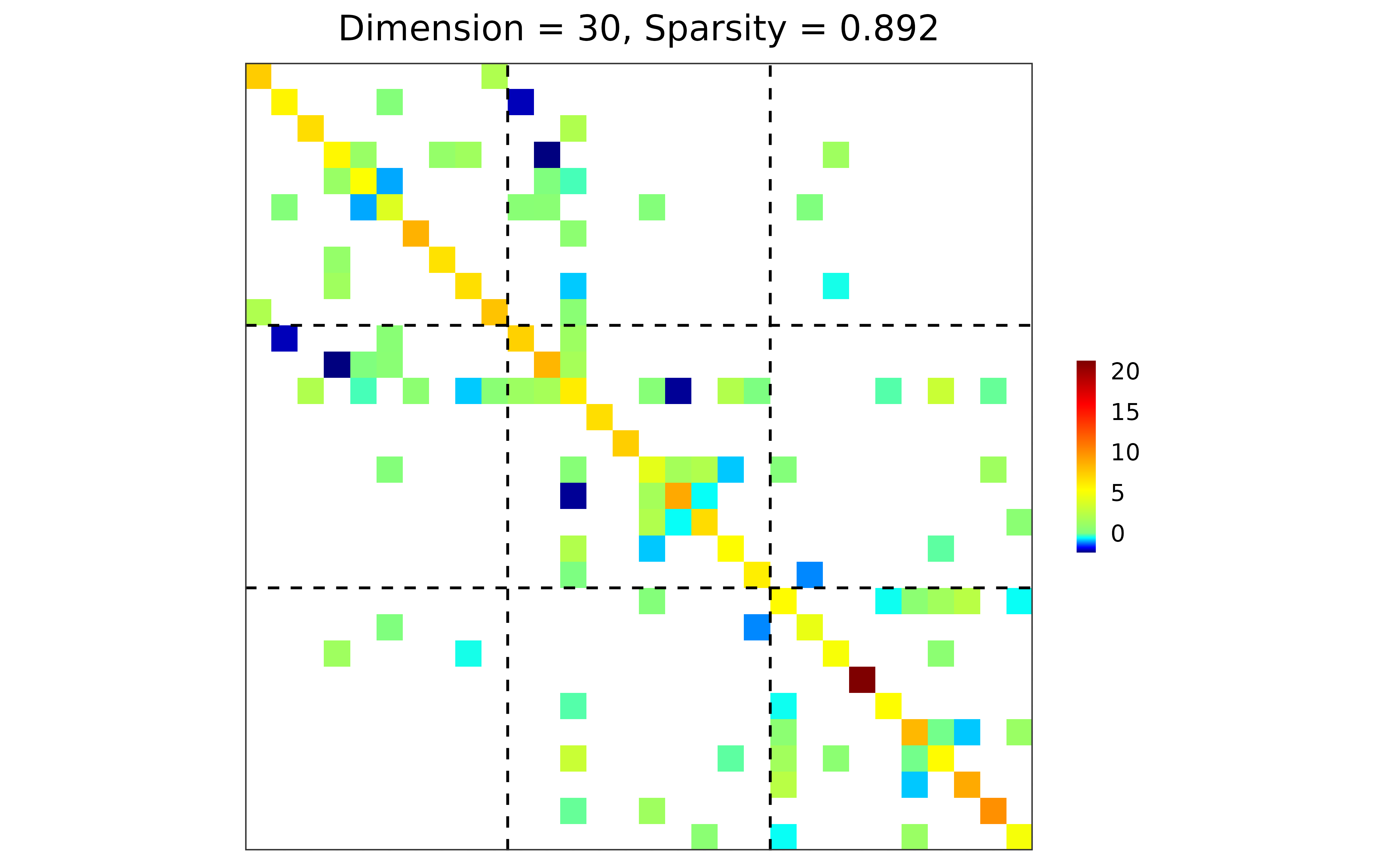## performance
performance(hatOmega = res$hatOmega, Omega = sim$Omega)
#>      measure    value
#> 1   sparsity   0.8920
#> 2  Frobenius  27.3885
#> 3         KL   7.9326
#> 4  quadratic  64.5716
#> 5   spectral  13.7645
#> 6         TP  19.0000
#> 7         TN 359.0000
#> 8         FP  28.0000
#> 9         FN  29.0000
#> 10       TPR   0.3958
#> 11       FPR   0.0724
#> 12        F1   0.4000
#> 13       MCC   0.3265